Coverage Control Problem

Introduction

Coverage control is the problem of navigating a robot swarm to collaboratively monitor features or a phenomenon of interest not known a priori. The goal is to provide sensor coverage based on the importance of information at each point in the environment. An importance density field (IDF) \(\Phi:\mathcal{W} \mapsto {R}_{\geq 0}\) is defined over a 2-D environment \(\mathcal W\subset R^2\). The IDF represents a non-negative measure of importance at each point in the environment. With the state of a robot \(i\) given by its position \(\mathbf p_i\in \mathcal W\) in the environment, the control actions given by the velocity \(\dot{\mathbf p}_i(t)\), and \(\Delta t\) as the time step, we use the following model for the state evolution:

\begin{equation} \mathbf p_i(t+\Delta t) = \mathbf p_i(t) + \dot{\mathbf p}_i(t) \Delta t. \end{equation}

Cost Function

The cost function for the coverage control problem is defined as:

\begin{equation} \mathcal J\left(\mathbf X\right) = \int_{\mathbf q \in \mathcal W} \min_{i\in\mathcal V} f(\|\mathbf p_i - \mathbf q\|) \Phi(\mathbf q)\,d\mathbf q. \label{eq:coverage_gen} \end{equation}

Here, \(f\) is a non-decreasing function, and a common choice is \(f(x) = x^2\) as it is a smooth function and is easy to optimize.

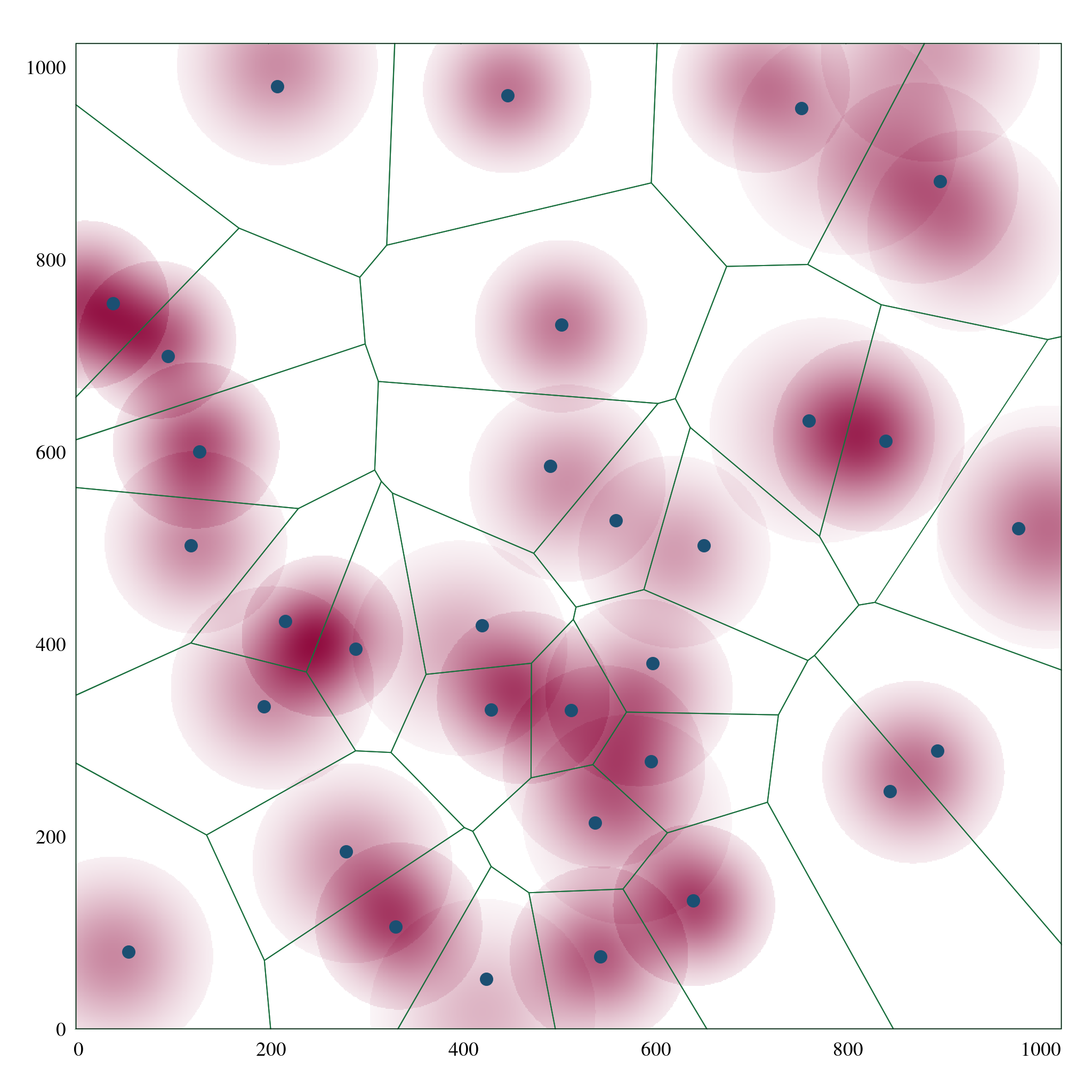
Assuming that no two robots can occupy the same point in the environment, the Voronoi partition can be used to assign each robot a distinct portion of the environment to cover. The Voronoi partition \(\mathcal P\) is defined as:

\begin{eqnarray*} \mathcal P &=& \{P_i \mid i \in \mathcal V\},\\ P_i &=& \{\mathbf q \in \mathcal W \mid \|\mathbf p_i - \mathbf q\| \le \|\mathbf p_j - \mathbf q\|, \forall j \in \mathcal V\}. \label{eq:voronoi} \end{eqnarray*}

All points in \(P_i\) are closer to robot \(i\) than any other robot. The cost function can now be expressed in terms of the Voronoi partition as:

\begin{equation} \mathcal J\left(\mathbf X\right) = \sum_{i=1}^N \int_{\mathbf q \in P_i} f(\|\mathbf p_i - \mathbf q\|) \Phi(\mathbf q)\,d\mathbf q. \label{eq:coverage_voronoi} \end{equation}

This new cost function is a sum of integrals over disjoint regions and is much easier to compute and optimize than the original function. Furthermore, if the Voronoi partition is known, the cost function can be computed in a decentralized manner, as each robot only needs to compute the integral over its own region \(P_i\).

The Problem

We can now define the coverage control problem in the context of the navigation control problem: Find a decentralized control policy \(\Pi\) that minimizes the expected cost \(\mathcal J(\mathbf X)\). The policy \(\Pi\) is defined over a space of all possible velocities, and each robot independently executes the same policy.

A near-optimal solution, along with Voronoi partition, to an instance of the coverage control problem with 32 robots and 32 features in a 1024 x 1024 environment.

Decentralized Coverage Control

The library aims at providing simulations and algorithms for the decentralized coverage control problem with the following restrictions:

The IDF \(\Phi\) is static and is not known a priori.
At any time, each robot can make localized observations of the IDF within a sensor field of view (FoV).
Each robot can maintain its own localized observations of the IDF aggregated over time.
The robots can only communicate with other robots that are within a limited communication radius.

In such a setting, a coverage control algorithm needs to provide the following based on the state of robot \(i\) and the information received from its neighbors \(\mathcal N(i)\):

A function \(\mathcal I\) that computes the information, in the form of messages, to be communicated by robot \(i\) to its neighbors, and
A common policy \(\Pi\) that computes the control action \(\mathbf u_i = \dot{\mathbf p}_i\) for any robot \(i \in \mathcal V\).

Designing such decentralized algorithms is challenging and can be intractable for complex systems. This motivates us to use a learning-based approach to design a decentralized coverage control algorithm. The LPAC Neural Network with GNN addresses the above challenges and provides a scalable and robust solution to the problem.

LPAC Architecture

Navigation of Robot Swarms

Navigating a swarm of robots through an environment to achieve a common collaborative goal is a challenging problem, especially when the sensing and communication capabilities of the robots are limited. These problems require systems with high-fidelity algorithms comprising three key capabilities: perception, action, and communication, which are executed in a feedback loop, i.e., the Perception-Action-Communication (PAC) loop. To seamlessly scale the deployment of such systems across vast environments with large robot swarms, it is imperative to consider a decentralized system wherein each robot autonomously makes decisions, drawing upon its own observations and information received from neighboring robots.

The Challenge

Designing a navigation algorithm for a decentralized system is challenging. The robots perform perception and action independently, while the communication module is the only component that can facilitate robot collaboration. Under limited communication capabilities, the robots must decide what information to communicate to their neighbors and how to use the received information to take appropriate actions. The motivation of designing this library is to study the coverage control problem as a canonical problem for the decentralized navigation of robot swarms. We develop the learnable PAC (LPAC) architecture that can learn to process sensor observations, communicate relevant information, and take appropriate actions.

Architecture

The learnable Perception-Action-Communication (LPAC) architecture is composed of three different types of neural networks, one for each module of the PAC system.

In the perception module, a convolution neural network (CNN) processes localized IDF observations and generates an abstract representation.
In the communication module, a GNN performs computation on the output of the perception module and the messages received from neighboring robots. It generates a fixed-size message to communicate with the neighbors and aggregates the received information to generate a feature vector for the action module of the robot.
In the action module, a shallow multilayer perceptron (MLP) predicts the control actions of the robot based on the feature vector generated by the GNN.

Learnable Perception-Action-Communication (LPAC) architecture: The three modules are executed on each robot independently, with the GNN in the communication module facilitating collaboration between robots.

‍LPAC: Learnable Perception-Action-Communication Loops with Applications to Coverage Control.
Saurav Agarwal, Ramya Muthukrishnan, Walker Gosrich, Vijay Kumar, and Alejandro Ribeiro.
arXiv preprint arXiv:2401.04855 (2024).

Table of Contents